Making sense of TypeScript using set theory
I've been working with TypeScript for a long long time. I think I'm not too bad at it. However, to my despair, some low-level behaviors still confuse me:
- Why does
0 | 1 extends 0 ? true : falseevaluate tofalse? - I'm very ashamed, but I sometimes confuse "subtype" and "supertype". Which is which?
- While we're at it, what are type "narrowing" and "widening", and how do they relate to sub/supertypes?
- If you want an object that satisfies both
{ name: string }and{ age: number }, do you&or|? Both make some sense, since I want a union of the functionality in both interfaces, but I also want the object to satisfy left & (and) right interfaces. - How is
anydifferent fromunknown? All I get is imprecise mnemonics like "Avoid Any, Use Unknown". Why? - What, exactly, is
never? "A value that never happens" is very dramatic, but not too precise. - Why
whatever | never === whateverandwhatever & never === never? - Why on earth is
const x: {} = true;valid TS code?trueis clearly not an empty object.
I was doing some research on never, and stumbled upon Zhenghao He's Complete Guide To TypeScript’s Never Type (check out his blog, it's super cool!). It mentions that a type is just a set of values, and — boom — it clicked. I went back to the basics, re-formulating everything I know about TS into set-theoretic terms. Follow me as I:
- Refresh my knowledge of set theory,
- Map TS concepts to their set counterparts,
- Start simple with booelan, null and undefined types,
- Extend to strings and numbers, finding some types that TS can not express,
- Jump into objects, proving my assumptions about them wrong,
- Finally gain confidence writing
extendscaluses, - And put
unknownandanywhere they belong.
In the end, I solve most of my questions, grow much cozier with TS, and come up with this brilliant map of TS types:
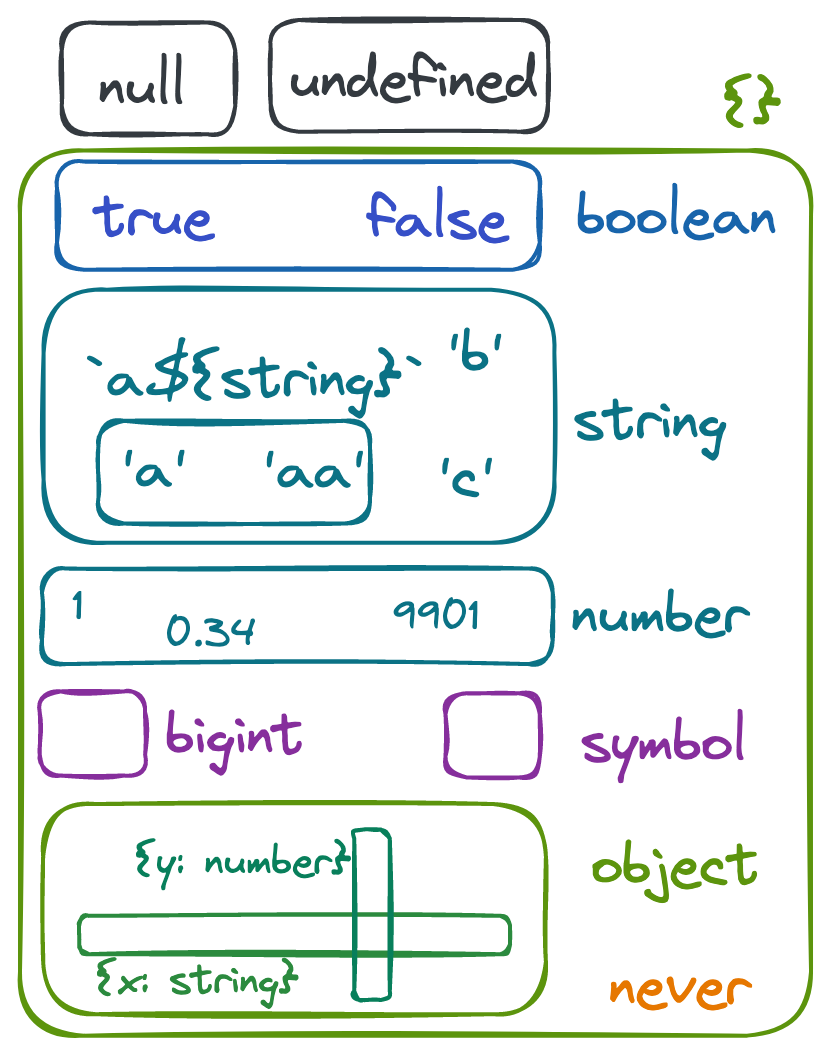
Set theory
First up, a refresher on set theory. Feel free to skip if you're a pro, but my algebra skills are a bit rusty, so I could use a reminder of how it works.
Sets are unordered collections of objects. In kindergarten terms: say we have two apples aka objects (let's call them ivan and bob, shall we?), and some bags aka sets where we can put the apples. We can make, in total, 4 apple sets:
- A bag with apple ivan,
{ ivan }— sets are written as curly brackets with the set items inside. - Similarly, you can have a bag with apple bob,
{ bob }. - A bag with both apples,
{ ivan, bob }. Hold onto your hats, this is called a universe because at the moment there's nothing in our world except these two apples. - An empty bag aka empty set,
{}. This one gets a special symbol, ∅
Sets are often drawn as "venn diagrams", with each set represented as a circle:

Apart from listing all the items, we can also build sets by condition. I can say "R is a set of red apples" to mean { ivan }, considernig ivan is red and bob is green. So far, so good.
Set A is a subset of set B if every element from A is also in B. In our apple world, { ivan } is a subset of { ivan, bob }, but { bob } is not a subset of { ivan }. Obviously, any set is a subset of itself, and {} is a subset of any other set S, because not a single item from {} is missing from S.
There are a few useful operators defined on sets:
- Union C = A ∪ B contains all the elements that are in A or in B. Note that A ∪ ∅ = A
- Intersection C = A ∩ B contains all the elements that are in A and B. Note that A ∩ ∅ = ∅
- Difference C = A \ B contains all the elements that are in A, but not in B. Note that A \ ∅ = A
This should be enough! Let's see how it all maps to types.
What does it have to do with types
So, the big reveal: you can think of "types" as sets of JavaScript values. Then:
- Our universe is all the values a JS program can produce.
- A type (not even a typescript type, just a type in general) is some set of JS values.
- Some types can be represented in TS, while other can not — for example, "non-zero numbers".
A extends Bas seen in conditional types and generic constraints can be read as "A is subset of B".- Type union,
|, and intersection,&, operators are just the union and intersection of two sets. Exclude<A, B>is as close as TS gets to a difference operator, except it only works when bothAandBare union types.neveris an empty set. Proof:A & never = neverandA | never = Afor any typeA, andExclude<0, 0> = never.
This change of view already yields some useful insights:
- Subtype of type A is a subset of type A. Supertype is a superset. Easy.
- Widening makes a type-set wider by allowing some extra values. Narrowing removes certain values. Makes geometrical sense.
I know this all sounds like a lot, so let's proceed by example, starting with a simple case of boolean values.
Boolean types
For now, pretend JS only has boolean values. There are exaclty two — true and false. Recalling the apples, we can make a total of 4 types:
- Literal types
trueandfalse, each made up of a single value; boolean, which is any boolean value;- The empty set,
never.
The diagram of the "boolean types" is basically the one that we had for apples, just the names swapped:

Let's try moving between type world and set world:
booleancan be written astrue | false(in fact, that's exactly how TS impements it).trueis a subset (aka sub-type) ofbooleanneveris an empty set, soneveris a sub-set/type oftrue,false, andboolean&is an intersection, sofalse & true = never, andboolean & true = (true | false) & true = true(the universe,boolean, doesn't affect intersections), andtrue & never = never, etc.|is a union, sotrue | never = true, andboolean | true = boolean(the universe,boolean, "swallows" other intersection items because they're all subsets of universe).Excludecorrectly computes set difference:Exclude<boolean, true> -> false
Now, a little self-assessment of the tricky extends cases:
type A = boolean extends never ? 1 : 0;
type B = true extends boolean ? 1 : 0;
type C = never extends false ? 1 : 0;
type D = never extends never ? 1 : 0;If you recall that "extends" can be read as "is subset of", the answer should be clear — A0,B1,C1,C1. We're making progress!
null and undefined are just like boolean, except they only contain one value each. never extends null still holds, null & boolean is never since no JS value can simultaneously be of 2 different JS types, and so on. Let's add these to our "trivial types map":
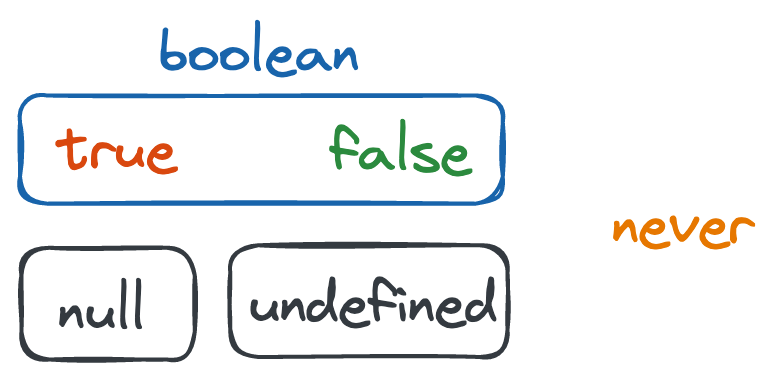
Strings and other primitives
With the simple ones out of the way, let's move on to string types. At first, it seems that nothing's changed — string is a type for "all JS strings", and every string has a corresponding literal type: const str: 'hi' = 'hi'; However, there's one key difference — there are infinitely many possible string values.
It might be a lie, because you can only represent so many strings in finite computer memory, but a) it's enough strings to make enumerating them all unpractical, and b) type systems can operate on pure abstrations without worrying about dirty real-life limitations.
Just like sets, string types can be constructed in a few different ways:
|union lets you constuct any finite string set — e.g.type Country = 'de' | 'us';. This won't work for infinite sets — say, all strings with length > 2 — since you can't write an infinite list of value.- Funky template literal types let you construct some infinite sets — e.g.
type V = `v${string}`;is a set of all strings that start withv.
We can go a bit further by making unions and intersections of literal and template types. Fun time: when combining a union with a template, TS is smart enough to just filter the literals againts the template, so that 'a' | 'b' & `a${string}` = 'a'. Yet, TS is not smart enough to merge templates, so you get really fancy ways of saying never, such as `a${string}` & `b${string}` (obviously, a string can't start with "a" and "b" at the same time).
However, some string types are not representable in TS at all. Try "every string except 'a'". You could Exclude<string, 'a'>, but since TS doesn't actually model string as union of all possible string literals, this in fact evaluates back to string. The template grammar can not express this negative condition either. Bad luck!
The types for numbers, symbols and bigints work the same way, except they don't even get a "template" type, and are limited to finite sets. It's a pity, as I could really use some number subtypes — integer, number between 0 and 1, or positive number. Anyways, all together:
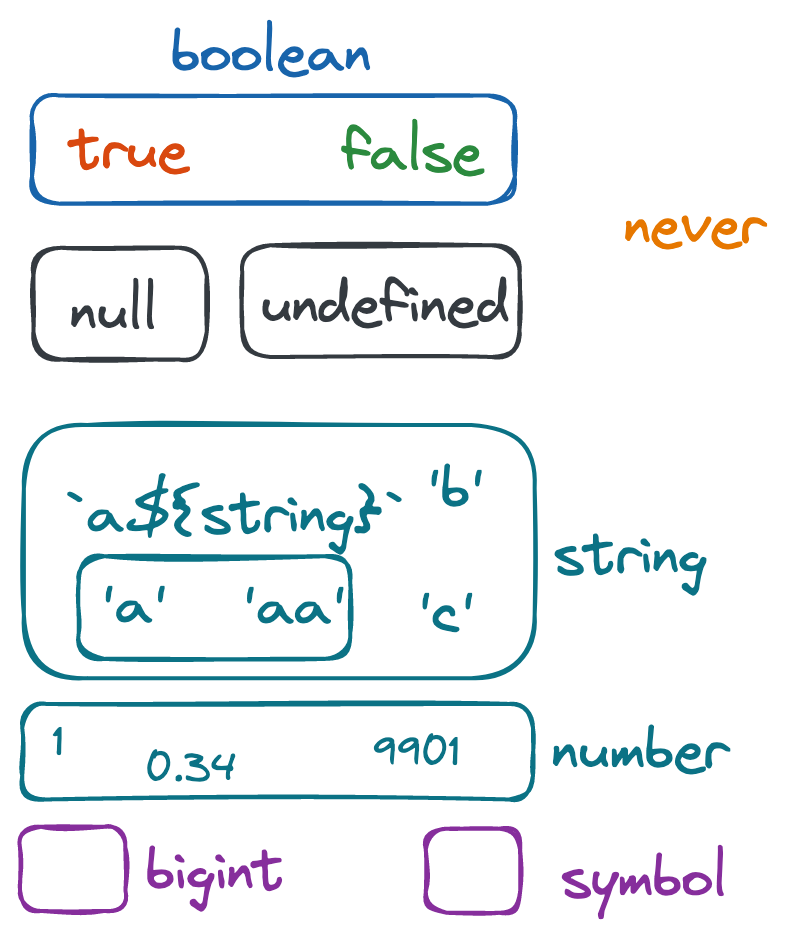
Phew, we've covered all primitive, non-intersecting JS / TS types. We've gotten comfortable moving between sets and types, and discovered that some types can't be defined in TS. Here comes the tricky part.
Interfaces & object types
If you think const x: {} = 9; makes no sense, this section is for you. As it appears, our mental model of what TS object types / records / interfaces was built on the wrong assumptions.
First, you'd probably expect types like type Sum9 = { sum: 9 } to act like "literal types" for objects — matching a single object value { sum: 9 }, adjusted for referential equality. This is absolutely not how it works. Instead, Sum9 is a "thing on which you can access propery sum to get 9" — more like a condition / constraint. This lets us call (data: Sum9) => number with an object obj = { sum: 9, date: '2022-09-13' } without TS complaining about unknown date property. See, handy!
Then, {} type is not an "empty object" type corresponding to a {} JS literal, but a "thing where I can access properties, but I don't care about any particular properties". Aha, now we can see what's going on in our initial mind-bender: if x = 9, you can safely x['whatever'], so it satisfies the unconstrained {} interface. In fact, we can even make bolder claims like const x: { toString(): string } = 9;, since we can x.toString() and actuallty get a string. More yet, keyof number gives us "toString" | "toFixed" | "toExponential" | "toPrecision" | "valueOf" | "toLocaleString", meaning that TS secretly sees our primitive type as an object, which it is (thanks to autoboxing). null and undefined do not satisfy {}, because they throw if you try to read a property. Not super intuitive, but makes sense now.
Coming back to my little "| or &" problem, & and | operate on "value sets", not on "object shapes", so you need { name: string } & { age: number } to get objects with both name and (extra hint: and = &) age.
Oh, and what about that odd object type? Since every property on an interface just adds a constraint to the "thing" we're typing, there's no way to declare an interface that filters out primitive values. It's why TS has a built-in object type that means specifically "JS object, not a primitive". Yes, you can intersect with object to get only non-primitive values satisfying an interface: const x: object & { toString(): string } = 9 fails.
Let's add all of these to our type map:

extends
extends keyword in TS can be confusing. It comes from the object-oriented world where you extend a class in the sense of adding functionality to it, but, since TS uses structural typing, extends as used in type Extends<A, B> = A extends B ? true : false is not the same extends from class X extends Y {}.
Instead, A extends B can be read as A is a sub-type of B or, in set terms, A is a subset of B. If B is a union, every member of A must also be in B. If B is a "constrained" interface, A must not violate any of B's constraints. Good news: a usual OOP class A extends B {} fits A extends B ? 1 : 0. So does 'a' extends string, meaning that (excuse the pun) TS extends extends extends.
This "subset" view is the best way to never mix up the order of extends operands:
0 | 1 extends 0is false, since a 2-element set{0, 1}is not a subset of the 1-element{0}(even though{0,1}does extend{1}in a geometrical sense).never extends Tis always true, becausenever, the empty set, is a subset of any set.T extends neveris only true if T isnever, because an empty set has no subsets except itself.T extends stringallows T to be a string, a literal, or a literal union, or a template, because all of these are subsets ofstring.T extends string ? string extends Tmakes sure that T is exactlystring, because that's the only way it can be both a subset and a superset of string.
unknown and any
Typescript has two types that can represent an arbitrary JS value — unknown and any. The normal one is unknown — the universe of JS values:
// It's a 1
type Y = string | number | boolean | object | bigint | symbol | null | undefined extends unknown ? 1 : 0;
// a shorter one, given the {} oddity
type Y2 = {} | null | undefined extends unknown ? 1 : 0;
// For other types, this is 0:
type N = unknown extends string ? 1 : 0;On a puzzling side, though:
unknownis not a union of all other base types, so you can'tExclude<unknown, string>unknown extends string | number | boolean | object | bigint | symbol | null | undefinedis false, meaning that some TS types are not listed. I suspectenums.
All in all, it's safe to think of unknown as "the set of all possible JS values".
any is the weird one:
any extends string ? 1 : 0evaluates to0 | 1which is basically a "dunno".- Even
any extends never ? 1 : 0evaluates to0 | 1, meaning thatanymight be empty.
We should conclude that any is "some set, but we're not sure which one" — like a type NaN. However, upon further inspection, string extends any, unknown extends any and even any extends any are all true, none of which holds for "some set". So, any is a paradox — every set is a subset of any, but any might be empty. The only good news I have is that any extends unknown, so unknown is still the universe, and any does not allow "alien" values.
So, to finish mapping our types, we wrap our entire diagram into unknown bubble:
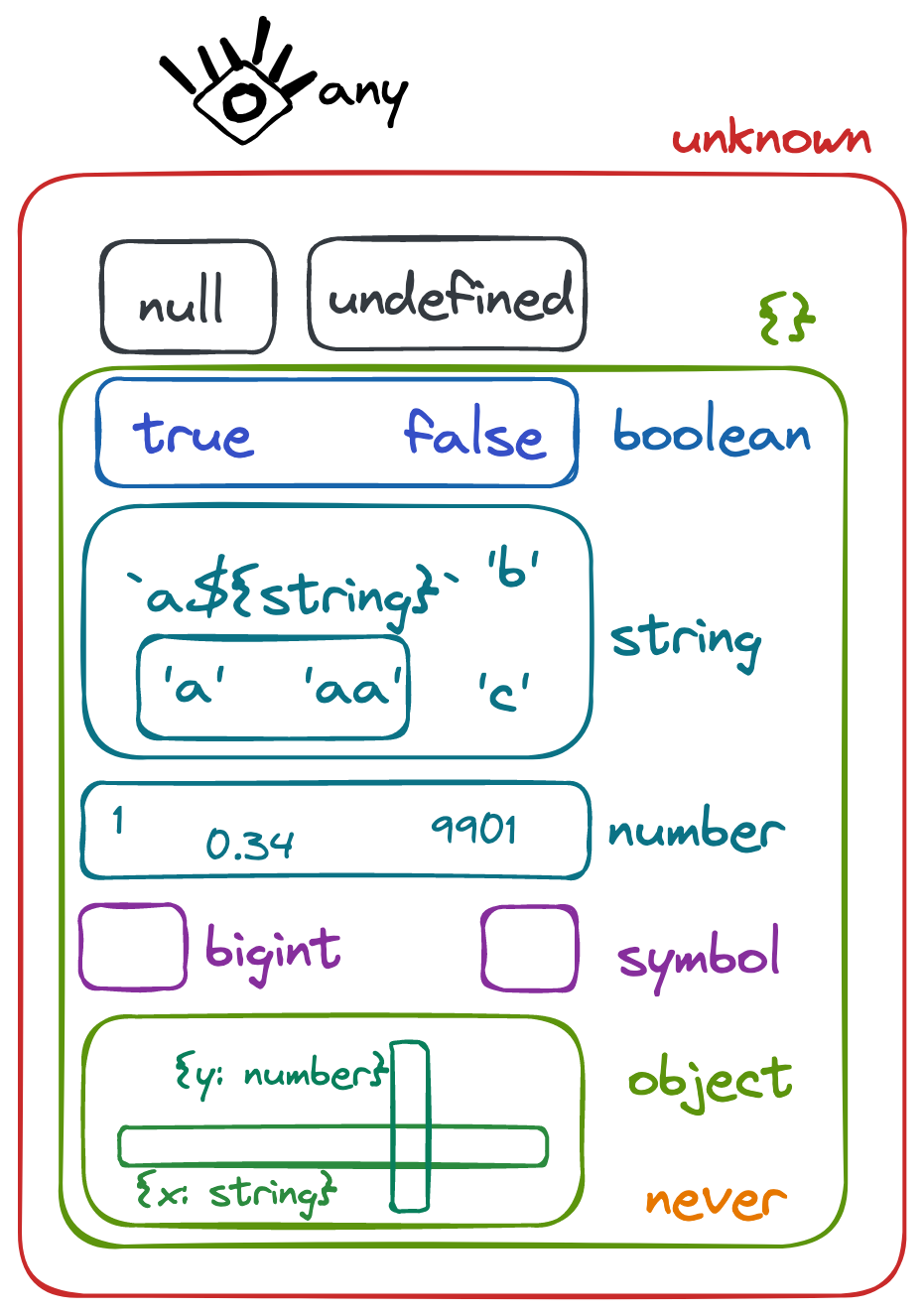
Today, we've learnt to that TS types are basically sets of JS values. Here's a little dictionary to go from type-world to set-world, and back:
- Our universe = all JS values = the type
unknown neveris an empty set.- Subtype = narrowed type = subset, supertype = widened type = superset.
A extends Bcan be read as "A is subset of B".- Union and intersection types are, really, just set union and intersection.
Excludeis an approximation of set difference that only works on union types.
Going back my our initial questions:
0 | 1 extends 0is false because {0,1} is not a subset of {0}&and|work on sets, not on object shapes.A & Bis a set of things that satisfy bothAandB.unknownis the set of all JS values.anyis a paradoxical set that includes everything, but might also be empty.- Intersecting with
nevergives youneverbecause it's an empty set.neverhas no effect in a union. const x: {} = true;works because TS interfaces work by constraining the property values, and we haven't constrained anything here, sotruefits.
We still have a lot of TS mysteries to solve, so stay tuned!
